| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- SOTA
- 프롬프트 잘 쓰는법
- chatgpt 꿀팁
- IT
- 경진대회
- GaN
- TabNet
- LLM
- Transformer
- LLM 성능 개선
- 프롬프트 페르소나
- 프롬프트 엔지니어링
- 프롬프트 잘 쓰는 법
- 악성댓글
- 프롬프트
- mergekit
- 머신러닝
- 강화학습
- ChatGPT 잘 쓰는 법
- GPT
- GPT3
- 인공지능
- 빅데이터
- AI
- 컴퓨터 비전
- ChatGPT
- 비전러닝
- 거대언어모델
- 모델링
- 딥러닝
- Today
- Total
빅웨이브에이아이 기술블로그
Neural Prophet, 1-step model 예제 본문
시작
안녕하세요! 빅웨이브에이아이 선임 연구원 이우창입니다.
지난번에는 Neural Prophet 모델에 대한 전반적인 내용을 소개드렸습니다.
이번에는 Neural Prophet 모델에서 AR(Auto Regression) 과정을 통해 1-step에 대한 데이터를 예측하기위해
학습 및 예측하기 위한 예제를 직접 실행해보겠습니다.
소스코드는 아래의 URL을 참조해주시면 됩니다.
https://colab.research.google.com/drive/1JoLECBglOebwh_JfyXle43QQMOSQWrkx?usp=sharing
NeuralProphet_Multivariate 1-step model2.ipynb
Colaboratory notebook
colab.research.google.com
패키지 및 데이터 임포트
<Neural Prophet 설치>
if 'google.colab' in str(get_ipython()):
! pip install git+https://github.com/ourownstory/neural_prophet.git # 코랩 구동 시 패키지 설치
# pip install neuralprophet
# 간단하고 빠르게 설치할 수 있지만, 최신 버전에서의 버그가 발생할 수 있음코랩에서는 실행마다 세션이 초기화되기 때문에 패키지를 새로 설치해야 합니다.
로컬에서 패키지를 성공적으로 설치하셨다면 스킵해도 되는 부분입니다.
지난 예제에서 설명드렸던 부분은 생략하고 넘어가겠습니다.
<패키지 임포트1>
#패키지 임포트
import pandas as pd
from neuralprophet import NeuralProphet, set_log_level
import plotly.express as px
import numpy as np
set_log_level("ERROR")지난번에는 numpy가 import가 안되어 있었는데, 이번 포스팅에는 numpy 패키지도 import할 수 있도록 추가
하였습니다.
<패키지 임포트2>
#구글 드라이브 다운로드 패키지
from google_drive_downloader import GoogleDriveDownloader as gdd
<데이터 다운로드 및 불러오기>
#데이터 다운로드
gdd.download_file_from_google_drive(file_id='1JRslcolP0XJDQKfXrYl82eyDTCETuzjl',
dest_path='data/energy.zip',
unzip=True)data = pd.read_csv('data/KAG_energydata_complete.csv').fillna(method='ffill').fillna(method='bfill')<데이터 변수 이름 설정>
#시계열 및 종속변수 이름 변경
data = data.rename(columns={"date":"ds","Appliances":"y"})
1-step AR(Auto Regression) model
AR model은 시계열 예측에서 주로 사용되는 자기 회귀 모형을 활용한 모델입니다.
본 포스팅에서 다룰 자기 회귀 모형은 1-step 즉, 이전 시간 단계의 데이터를 모델이 학습하여 다음 시간 단계에
대한 예측을 위해 사용됩니다.
AR(1)모델 설계를 위해 데이터와 같은 경우 y데이터와 y데이터를 lag시킨 데이터 'l'을 생성하였습니다.
<분석 변수 설정 및 전처리>
#y와 y의 t-1시점 데이터만을 사용
df = data.copy(deep=True)
df["l"]= np.append(0, data["y"].values[:-1])
df=df[['ds','y','l']]
df.tail(3)<모델 설계 및 학습>
m = NeuralProphet(
growth='off', # 추세 유형 설정(linear, discontinuous, off 중 선택 가능)
yearly_seasonality=False, #년간 계절성 설정
weekly_seasonality=False, #주간 계절성 설정
daily_seasonality=False, #일간 계절성 설정
batch_size=64,#배치 사이즈 설정
epochs=100,#학습 횟수 설정
learning_rate=0.1, # 학습률 설정
#n_lags= 1, #데이터를 이미 lag 데이터를 생성하였으니 옵션을 설정하지 않음
)
#독립 변인(변수) 추가 및 정규화
m = m.add_lagged_regressor(names=["l"], normalize="minmax")
#학습데이터, 검증데이터 분리
train, test = m.split_df(df, freq='H', valid_p = 0.10)
#학습 수행
metrics = m.fit(train, freq='h', validation_df=test, progress='plot')모델 설계에서는 MAE를 최대한 낮출 수 있도록 파라미터를 조정하였으며, AR(1)모델 설계를 위해 주간, 일간,
년 간 계절성에 대한 설정을 배제하였습니다. 또한 추세유형은 off로 설정하였으며, 여기서 1-step이 아니라, 2-step, ... n-step에 대한 학습을 예측을 원한다면 해당 인수로 설정할 수 있습니다.
add_lagged_regressor에서는 AR(1) 모형을 설계하므로 y데이터의 lag된 변수 "l"만을 설정합니다.
<Metric 확인>
metrics.tail(3)
<주요 성능 지표 확인>
#metric 확인
#print("SmoothL1Loss: ", metrics.SmoothL1Loss.tail(1).item())
print("MAE(Train): ", metrics.MAE.tail(1).item())
print("MAE(Test): ", metrics.MAE_val.tail(1).item())
<Train 및 Test 학습 선 그래프 생성>
#학습 선 그래프 생성
px.line(metrics, y=['MAE', 'MAE_val'], width=800, height=400)
시각화 검증
<검증 데이터의 실제값 및 예측값 시각화 비교>
#yhat1과 실제값 시각화(lag 데이터 포함x)
forecast = m.predict(test)
fig = m.plot(forecast[['ds', 'y', 'yhat1']])
실제값과 예측값을 비교해본 결과, 이상치나 y의 값이 낮은 경우 예측이 잘 되지 않는 모습이 나타납니다.
y에 대한 예측은 70~200수준 안에서만 예측이 되는것으로 보이며, 전체적으로 예측에 대한 성능이 좋지 못한 것으로 보입니다.
#yhat1과 실제값 시각화(lag 데이터 포함O)
forecast = m.predict(test)
m = m.highlight_nth_step_ahead_of_each_forecast(1)
fig = m.plot(forecast)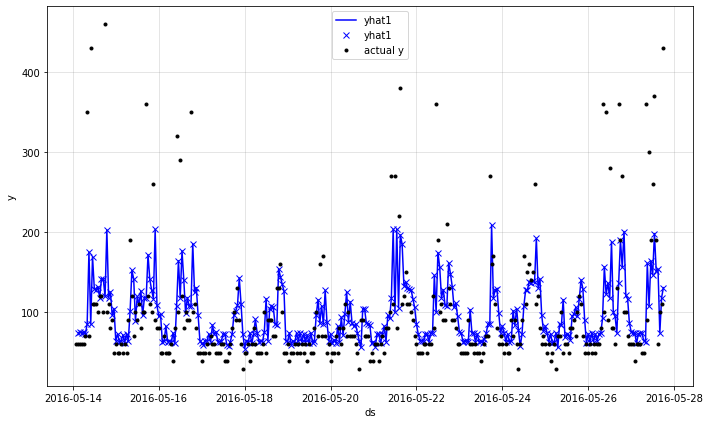
다음 결과 값은 lag된 데이터를 포함한 결과입니다.
<1-step AR(1)모델에 대한 Components 시각화>
#1-ahead에 대한 변수별 components 시각화
fig_comp = m.plot_components(forecast)
1-step AR : Using Neural Network
AR-Net은 시계열 예측에서 주로 사용되는 자기 회귀 모형에서 최소 하나 이상의 은닉층을 고려한 신경망 모델
입니다. 본 포스팅에서 다룰 자기 회귀 신경망 네트워크는 은닉층을 사용하여 1-step 즉, 이전 시간 단계의 데이터를 모델이 학습하여 다음 시간 단계에 대한 예측을 위해 사용됩니다.
m = NeuralProphet(
growth='off', # 추세 유형 설정(linear, discontinuous, off 중 선택 가능)
yearly_seasonality=False, #년간 계절성 설정
weekly_seasonality=False, #주간 계절성 설정
daily_seasonality=False, #일간 계절성 설정
batch_size=64,#배치 사이즈 설정
epochs=100,#학습 횟수 설정
learning_rate=0.001, # 학습률 설정
#n_lags= 1, #데이터를 이미 lag 데이터를 생성하였으니 옵션을 설정하지 않음
num_hidden_layers=4, #히든 레이어 수 설정
d_hidden=8,#은닉층에 대한 차원 수 설정
)
#독립 변인(변수) 추가 및 정규화
m = m.add_lagged_regressor(names=["l"], normalize="minmax")
#학습데이터, 검증데이터 분리
train, test = m.split_df(df, freq='H', valid_p = 0.10)
#학습 수행
metrics = m.fit(train, freq='h', validation_df=test, progress='plot')이전의 1-step AR(1) 모델과 대비하여 히든 레이어(은닉층)을 설정한 모델입니다. 여기서 은닉층의 수는 4개,
차원 수는 8개로 설정하였습니다. 1-step AR(1)모델과 마찬가지로 n_lag=1로 설정하였으며, 나머지 옵션들은
비교를 위해 이전 모델과 통일하였습니다.
<주요 성능 지표 확인>
#metric 확인
print("SmoothL1Loss: ", metrics.SmoothL1Loss.tail(1).item())
print("MAE(Train): ", metrics.MAE.tail(1).item())
print("MAE(Test): ", metrics.MAE_val.tail(1).item())<Train 및 Test 학습 선 그래프 생성>
#학습 선 그래프 생성
px.line(metrics, y=['MAE', 'MAE_val'], width=800, height=400)
은닉층을 추가하지 않은 경우와 비교하였을 때, train 과 test 데이터의 MAE가 좀 더 안정적이게 감소 하는 것으로 보입니다.
시각화 검증
#yhat1과 실제값 시각화(lag 데이터 포함x)
forecast = m.predict(test)
fig = m.plot(forecast[['ds', 'y', 'yhat1']])
은닉층을 추가하지 않았을 때와 비교하였을 때, 이상치들을 조금더 잡아내는 모습을 보이며, 정확도가 개선되었음을 시각적으로 확인할 수 있었습니다.
#yhat1과 실제값 시각화(lag 데이터 포함O)
forecast = m.predict(test)
m = m.highlight_nth_step_ahead_of_each_forecast(1)
fig = m.plot(forecast)
#1-ahead에 대한 변수별 components 시각화
fig_comp = m.plot_components(forecast)
마무리
이번 포스트에서는 Neural Prophet모델을 활용한 1-step 예측을 위한 수행했습니다.
AR(1)과정을 활용하여 Neural Prophet 모델로 분석을 수행할 수 있었습니다.
추후에는 AR(1)과정 뿐만 아니라, AR(2), ... AR(n) 과정에 대한 모델을 전체적으로 수행하여 정확도를 분석해보면 좀 더 좋은 결과를 얻을 수 있을 것이라 기대됩니다.
읽어주셔서 감사합니다!
'Python 코드 예제' 카테고리의 다른 글
| Neural Prophet, 모델 최적화 (9) | 2022.05.09 |
|---|---|
| Neural Prophet, Multivariate 예제 (9) | 2022.03.17 |
| (Python code) 딥러닝 기술을 활용한 악성 댓글 분류 (2) | 2021.03.09 |



