| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 프롬프트 잘 쓰는 법
- mergekit
- IT
- 머신러닝
- 경진대회
- 컴퓨터 비전
- 비전러닝
- 모델링
- 빅데이터
- Transformer
- 프롬프트
- ChatGPT
- 프롬프트 잘 쓰는법
- SOTA
- GPT3
- 거대언어모델
- 강화학습
- 악성댓글
- 프롬프트 엔지니어링
- 인공지능
- GPT
- LLM 성능 개선
- AI
- chatgpt 꿀팁
- LLM
- 프롬프트 페르소나
- ChatGPT 잘 쓰는 법
- GaN
- 딥러닝
- TabNet
- Today
- Total
빅웨이브에이아이 기술블로그
SOTA 알고리즘 리뷰 1 - Temporal Fusion Transformer 본문
안녕하세요! 빅웨이브에이아이의 이현상입니다.
인공지능 분야에서는 특정 분야에 대해 가장 높은 성능을 달성한 모델을 SOTA 알고리즘이라고 부르기도 합니다.
즉, 모델 성능이 예술의 경지에 도달했다고 할 만큼 좋은 성능을 가지고 있는 모델이라는 것입니다.
AI 분야는 최신 SOTA 기술을 활용하는 것이 모델의 성능에 영향을 미치기 때문에 아주 중요한 요소가 됩니다.
읽어주시는 분들에게 더욱 유용한 정보를 드리고자 "SOTA 알고리즘 리뷰" 시리즈를 포스트할 계획입니다.
오늘은 시계열 분석 분야의 SOTA(State Of The Art) 알고리즘인 TFT(Temporal Fusion Transformer)에 대해서 알아보겠습니다.
핵심 아이디어 위주로 간단하게 설명 드리겠습니다.
Key Idea
2019년 Google Cloud AI와 영국 옥스포드 대학이 함께 발표한 논문 Lim et al. (2019)은 시계열 분석에 있어서 획기적인 아이디어를 제시했습니다.
시계열 분석이란 지난 포스트(고객 이탈 예측)의 데이터와 같이 시간적인 순서를 가지고 있는 정보에 대해서 예측 모델을 만드는 것입니다.
예를 들어, 시간적 순서를 가지고 있는 전기 소비량, 교통량, 판매량, 휘발유량, 주가, 비트코인 가격 등을 일련의 time step(시간 단위)을 가지고 예측합니다.
시계열 데이터는 time step을 기준으로 구성되며 분석가는 몇개의 time step을 가지고 얼마 후의 시점을 예측할 지 결정해야 합니다.
만약 예측 시점 간격이 1일이라면 1일 후 전기 소비량을 예측하는 방식으로 입력 데이터 및 모델이 구성됩니다.
시계열 분석을 통해 미래의 정보를 비교적 정확하게 알 수 있다면 정말 유용하게 사용할 수 있을 것입니다.
밑의 그림은 시계열 예측 분석 결과 예시로 과거 데이터를 학습하여 미래의 결과를 예측하는 방식입니다.
X축이 시점에 해당하고 Y축이 예측 수치를 의미하며 파란 선이 실제 값, 빨간 선이 예측 값에 해당합니다.
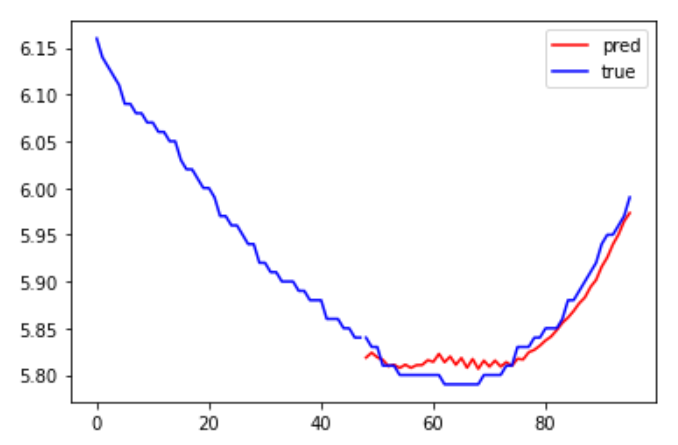
그런데 기존 시계열 분석 기법은 예측 시점 간격이 길어질수록 목표값 예측이 어렵다는 문제점이 있습니다.
왜냐하면 예측 모델에 미래의 어떤 정보도 활용하지 못한 채 긴 시퀀스를 예측해야 하기 때문입니다.
만약 바로 다음 time step 시점의 목표값을 예측한다면 바로 전 시점 데이터를 활용할 수 있기 때문에 비교적 쉬운 task가 됩니다.
본 논문에서는 이 점을 지적하면서 미래 시점에 미리 알 수 있는 정보들을 활용할 수 있도록 딥러닝 모델을 구성했습니다.
한 주의 요일, 월, 휴일, 미리 계획된 사항 등에 관련된 변수들은 미래에도 이미 알 수 있는 변수들입니다.
이를 장기적인 시간 정보를 가지고 있는 데이터를 분석할 때 활용할 수 있다면, time step이 길어지더라도 우수한 성능으로 예측할 수 있습니다.
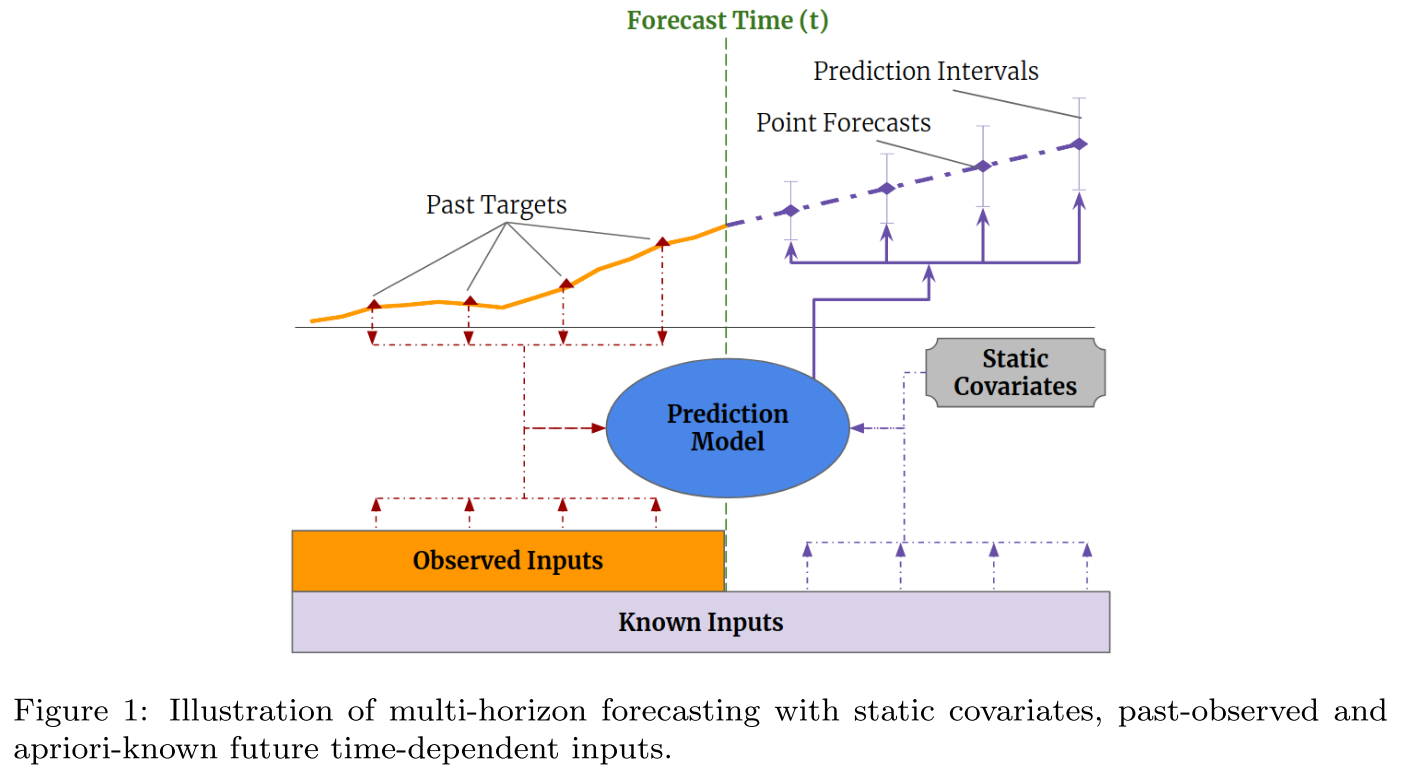
위의 그림을 보시면 미래에는 알 수 없는 관측 변수(Observed Inputs)들과 함께 알고 있는 변수(Known Inputs)들을 같이 활용합니다.
관측 변수의 경우 일반적인 시계열 분석에 활용되는 것처럼 예측 모델(Prediction Model)에 입력됩니다.
미래 시점의 알고 있는 변수들과 정적 공변량이 함께 예측 모델에 입력되어 다중 시점(multi-horizon) 예측 시 활용됩니다.
여기서 정적 공변량이란 표현은 하나의 값으로 고정되어 있는 변수들(ex: 위치, 타입 등)을 의미합니다.
하나의 값으로 고정되어 있기 때문에 당연히 미래에도 같은 값으로 입력되겠죠?
기존 시계열 분석 기법의 문제점을 잘 파악하여 훌륭한 개선점을 도출했다고 볼 수 있습니다.
모델링
전체적인 모델 아키텍처의 프로세스 부터 설명 드리겠습니다.
우선 시계열 데이터 중 관측 변수는 과거 시점의 LSTM 인코더에 입력됩니다.
알고 있는 변수는 과거 시점과 함께 미래 시점의 LSTM 디코더에 같이 입력됩니다.
정적 공변량은 고정되어 있는 변수기 때문에 변수 선정 네트워크, LSTM 인코더, GRN을 통해 충분한 정보를 전체 레이어에 전달합니다.
모든 변수는 선정 네트워크 과정을 거치며 매 시점마다 평가되어 중요한 변수만 모델에 입력되는 방식입니다.
일련의 프로세스를 거친 입력 정보들은 Masked Interpretable Multi-Head Attention Layer에 전달됩니다.
Attention Layer에서 산출된 정보는 Position-Wise Feed-Forward 비선형 레이어(GRN)을 거쳐서 입력됩니다.
최종 출력값은 LSTM 디코더의 출력 정보를 반영하여 모델의 복잡성을 완화합니다.
모델링 전반적으로 게이팅 메커니즘을 통해 네트워크의 복잡성 문제를 해결하는 방식이 보입니다.
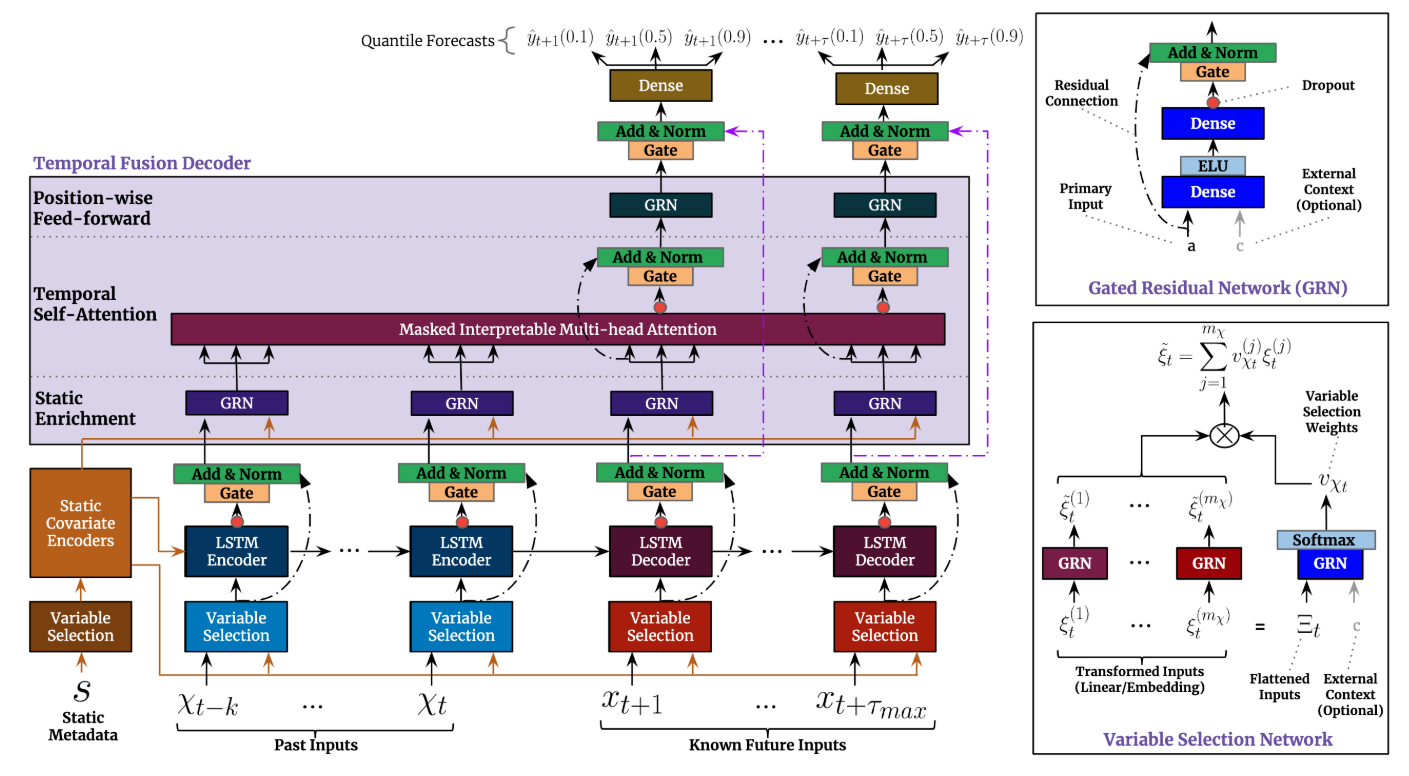
알고리즘 설명
TFT 모델링 기법에 적용된 분석 알고리즘들을 정리해보겠습니다.
1. 게이팅 메커니즘(Gating Mechanisms)
모델 학습 시 과거 데이터 중 불필요한 시점의 입력을 통제하여 장기간 예측을 유리하게 함
2. 변수 선정 네트워크(Variable Selection Networks)
각 time step마다 적절한 입력 변수 선정
3. 정적 공변량 인코더(Static Covariate Encoders)
정적 공변량을 모델에 입력할 수 있는 형태로 통합하여 context vector로써 동적 변수의 조건으로 설정
4. Temporal Processing
관측 및 알고 있는 변수를 장단기 예측에 입력하기 위한 시점 처리, 해석 가능한 multi-head attention 기법 적용
5. 예측 시점 구간(Prediction Intervals)
각 예측 시점마다 목표 변수의 범위를 결정하기 위한 분위수(quantile) 예측
하나씩 자세하게 설명드리겠습니다.
게이팅 메커니즘(Gating Mechanism)
게이팅 메커니즘은 지난 포스트에서 LSTM을 설명 드린 바와 같이 장기간 시퀀스에서 필요 없는 정보를 망각하고, 필요한 정보를 모델에 입력하도록 유도합니다.
이 과정에서 입력 시퀀스가 긴 데이터라도 안정적으로 모델을 학습할 수 있습니다.
하지만 입력 시퀀스 중 유용한 정보를 가지고 있는 시점을 가려내는 일은 어렵습니다.
특히 비선형 모델의 경우 구조가 더욱 복잡하기 때문에 모델의 성능을 떨어뜨릴 수 있습니다.
그래서 TFT에서는 GLU(Gated Linear Units)를 적용한 GRN(Gated Residual Network)라는 기법을 활용합니다.
Residual Network는 딥러닝 네트워크에서 중간 레이어를 스킵(skip connection)하여 잔차(residual)를 연결하는 방식으로 과적합을 방지해주는 효과가 있습니다.
GRN에서는 주요 변수와 optional context vector를 입력 후 게이트를 통과하여 레이어가 표준화(Norm) 됩니다.
이 때, 주요 변수의 잔차에 대해 게이트를 통과한 결과 값을 GLU를 통해 추가해줍니다(Add).
GLU는 시그모이드 활성화 함수 및 Hadmard Product 행렬 연산을 활용한 활성화 함수입니다.
GLU 기법은 게이트의 입력 차단 시 비선형 기여(nonlinear contribution)을 막기 위해 활용됩니다.
GRN 기법은 TFT의 거의 모든 레이어에서 적용되며 모델의 복잡성 문제를 보정합니다.
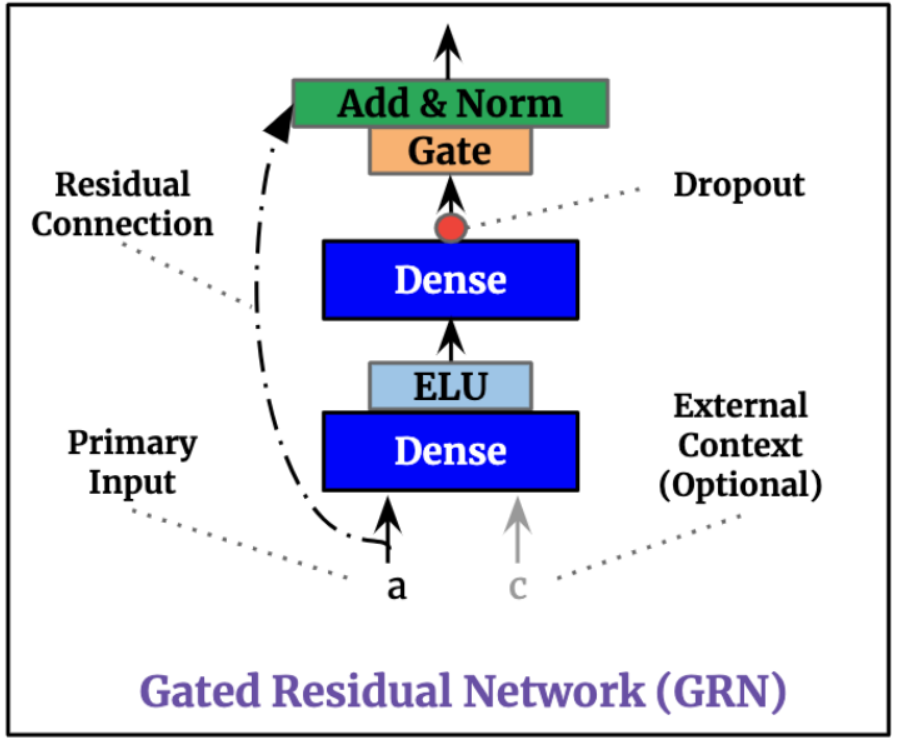
변수 선정 네트워크(Variable Selection Networks)
예측 모델에 변수가 너무 많을 경우 주요 변수의 영향을 놓쳐서 성능에 악영향을 끼칠 수 있습니다.
특히, 시계열 예측 분석에서 변수를 선정하는 프로세스는 모델 성능 향상에 큰 효과를 미칠 수 있습니다.
TFT 모델에서는 정적 공변량 및 시간 종속(time-dependent) 공변량을 둘 다 적용한 instance-wise 변수 선정 네트워크 기법을 제시합니다.
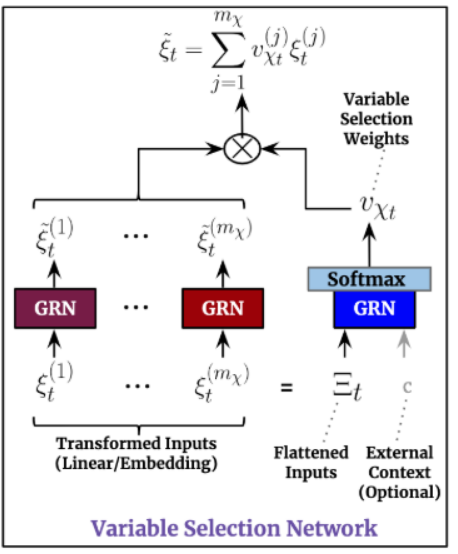
변수 선정 네트워크 모델에는 통합된 전체 입력 변수, 외부 context vector를 GRN에 입력 후 Softmax를 통해 변수를 선정(1)합니다.
추가적으로 전체 입력 변수 각각에 대해서도 GRN 모델을 적용(2)합니다.
최종적으로 (1), (2) 모델을 통합하여 t 시점의 활용 변수를 선정합니다.
변수 선정 네트워크 모델은 딥러닝 모델의 잡음(noisy)을 효과적으로 제어하여 모델의 성능을 크게 높일 수 있습니다.
정적 공변량 인코더(Static Covariate Encoders)
TFT 모델은 다른 시계열 분석 기법과 다르게 정적 메타데이터 정보를 통합하는 방식으로 설계되었습니다.
분리된 형태의 GRU 인코더들이 4개의 context vector를 생성합니다.
이 컨텍스트 벡터들은 TFT의 디코더에 다양한 방식으로 활용됩니다.
(선정된 시간 변수, 로컬 시점에서 처리된 시간 변수, 고정 변수 관련 컨텍스트 벡터)
각 컨텍스트 벡터는 GRN을 통해 모델에 인코딩 됩니다.
Temporal Processing
Temporal Processing에서는 attention 및 모델 디코더에 관련된 내용들로 구성되어 있습니다.
attention에 관련된 내용은 지난 포스트에서도 다뤘기 때문에 참고하시면 좋을 것 같습니다.
1. Interpretable Multi-Head Attention
TFT 모델에서는 장기간 time step을 학습시키기 위해 트랜스포머(transformer) 기반의 multi-head attention 기법을 설명력을 강화하는 방식으로 적용했습니다.
일반적으로는 multi-head attention 시 각 head의 attention 가중치가 각기 다르기 때문에 특성의 중요도를 추출하기 어렵습니다.
그래서 TFT에서는 각 head 간의 attention 가중치 값을 공유하는 방식으로 특성의 중요도를 추출했습니다.
새로운 attention 가중치 계산 방식으로 transformer 기반 attention 메커니즘의 설명력을 높인 것입니다.
2. Locality Enhancement with Sequence-to-Sequence Layer
시계열 분석에서는 일반적으로 목표값의 시점에 가까울수록 특성의 중요도가 향상됩니다.
목표값의 해당 시점의 로컬 컨텍스트를 활용하면 attention 기반 모델의 성능이 향상될 수 있습니다.
하지만 TFT 모델의 입력 값은 출력 값의 길이와 다르기 때문에 Seq2Seq 모델 방식으로 접근해야 합니다.
결론적으로 TFT 모델은 LSTM 인코더, 디코더 구조를 통해 locality를 강화합니다.
3. Static Enrichment Layer
때로는 고정 변수의 영향이 전체 예측 모델에서 중요한 역할을 할 수도 있습니다.
이러한 경우 이를 충분히 모델에 반영하고자 TFT는 고정 변수의 컨텍스트 벡터를 GRN 모델을 통해 전체 레이어에 전달합니다.
4. Temporal Self-Attention Layer
Static Enrichment 과정 후에는 이제 self-attention을 적용해야 합니다.
다른 트랜스포머 기법 구조와 비슷하게, 디코더 시점에서 masking을 수행하여 temporal 차원이 특성에만 집중하도록 합니다.
또한 인과적인 정보 흐름을 보존하고 장거리 시점의 종속성도 제대로 포착하여 장기간 예측에 유리합니다.
5. Position-wise Feed-Forward Layer
TFT 모델에서는 self-attention layer에 추가적인 비선형 레이어 프로세스를 하나 추가했습니다.
역시 GRN으로 구성되며 전체 레이어 구조에 가중치가 전파됩니다.
또한, 전체 트랜스포머 레이어와 Seq2Seq 레이어를 직접 연결하는 경로를 설정하여 모델의 복잡성 문제를 해결했습니다.
예측 시점 간격
TFT는 예측 시점에 예측 간격을 생성하는 방식을 사용합니다.
매 시점마다 10% 분위수, 50% 분위수, 90% 분위수를 동시에 예측합니다.
이러한 Quantile(분위수) 예측은 temporal fusion decoder의 선형 변환으로 인해 생성됩니다.
TFT 모델 벤치마크 테스트
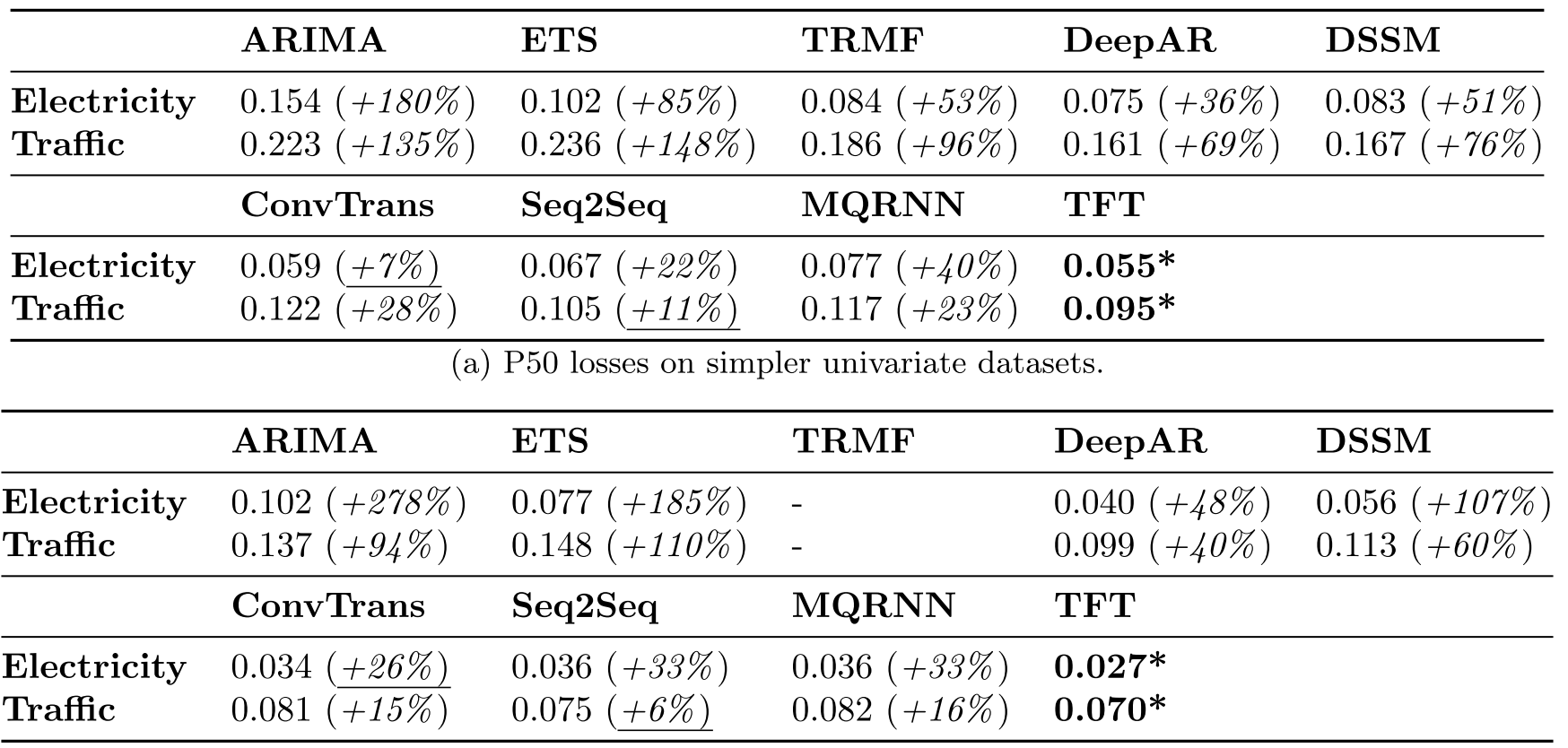
결과적으로 시계열 분석에 사용되는 일반적인 머신러닝 및 딥러닝 기법 보다 우수한 성능을 나타냈습니다.
마무리
이번 포스트에서는 시계열 분석 분야에서 좋은 평가를 받고 있는 TFT 모델에 대해서 설명드렸습니다.
시계열 분석 분야에서 트랜스포머 구조를 활용하기 위해 아주 디테일한 부분까지도 신경을 쓴 모델 아키텍처입니다.
모델 구조가 다소 복잡하지만 게이팅 메커니즘을 통해 모델의 복잡성 문제를 완화시켜 실제 장기간 예측에서 효과적인 모습이 보입니다.
하지만 제가 실제로 모델을 직접 테스트했을 때 모델 성능이 약간 아쉬운 부분이 있었습니다.
제 생각에는 모델 복잡성 문제 해결을 위해 조금 더 효과적인 방법론이 필요하다고 생각합니다.
아무래도 직접 번역한 것이다 보니 틀린 부분이나 어색한 부분이 있을지도 모르겠습니다.
지적은 언제든 환영이니 댓글로 달아주시면 감사하겠습니다!
앞으로 TFT와 같은 딥러닝 관련 SOTA 알고리즘들을 기술 블로그에서 소개드릴 예정입니다.
한번씩 들러주시면 감사하겠습니다.
'기술 블로그' 카테고리의 다른 글
| SOTA 알고리즘 리뷰 3 - TabNet (2) | 2021.06.25 |
|---|---|
| SOTA 알고리즘 리뷰 2 - Anomaly detection(PANDA, DEVNET, GAN,OCNN) (0) | 2021.06.18 |
| 고객 이탈 방지 시스템 (2020 AI Championship 2등) (5) | 2021.03.22 |
| Know Comment API - 차별 및 혐오 표현 탐지 솔루션 (2) | 2021.03.19 |
| 딥러닝 기술을 활용한 악성 댓글 분류 (2020 인공지능 온라인 경진대회 1등) (0) | 2021.03.09 |




